Bayesian Regression using PyMC3

Linear regression

$\begin{eqnarray} y_i= \boldsymbol{x}_i^T \boldsymbol{w} +n_i \\ \end{eqnarray}$
Here, $n_i \sim \mathcal{N}(0, \sigma^2)$ . Therefore, we can re-write $y_i$ as:
$\begin{eqnarray} y_i\sim\mathcal{N}(\boldsymbol{x}_i^T \boldsymbol{w}, \sigma^2) \end{eqnarray}$

In Bayesian linear regression, we assume $y_i, \boldsymbol{x}_i$ as data and $\boldsymbol{w}, \sigma^2$ as parameters. Therefore, the likelihood is as follows:
$\begin{eqnarray} \text{likelihood} = p(y| \boldsymbol{x},\boldsymbol{w},\sigma)=\prod_{i=1}^n p(y_i| \boldsymbol{x}_i,\boldsymbol{w},\sigma) \end{eqnarray}$

Using Bayes rule, the posterior distribution can be written as:
$\begin{eqnarray} p(\boldsymbol{w},\sigma|y, \boldsymbol{x})=\dfrac{ p( y|\boldsymbol{w},\sigma, \boldsymbol{x})p(\boldsymbol{w},\sigma|\boldsymbol{x})}{p(y|\boldsymbol{x})} \propto p( y|\boldsymbol{w},\sigma, \boldsymbol{x})p(\boldsymbol{w},\sigma|\boldsymbol{x})\\ p(\boldsymbol{w},\sigma|y)\propto p( y|\boldsymbol{w},\sigma)p(\boldsymbol{w},\sigma)~~~[\text{re-writing without }\boldsymbol{x}] \end{eqnarray}$

Now, we can assume $\boldsymbol{w}$ and $\sigma$ to be independent of each other. We can further assume, all the elements of $\boldsymbol{w}=\left[w_1, \ldots, w_m\right]$ are independent. Therefore, prior can be written as:

$\begin{eqnarray} p(\boldsymbol{w},\sigma) = \prod_j p(w_j) ~p(\sigma) \end{eqnarray}$

Prior Distribution

When ${w_j}\sim\mathcal{N}\left(0,\dfrac{\sigma^2}{\lambda }\right)$ , then the MAP estimate is ridge regression.
When $p(w_j)=\dfrac{1}{2(\sigma^2 / \lambda)}\exp\left(-\dfrac{|w_j|}{ \sigma^2 / \lambda}\right)$ , i.e. Laplacian distribution, then the MAP estimate is the lasso regression.

Linear Regression using sklearn

First we import all the necessary functions:

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("whitegrid")
sns.set_context("poster")

from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso, LassoCV
from sklearn.linear_model import Ridge, RidgeCV
import pymc3 as pm

We are generating some data points for the function $y= x_1 + x_2 + x_3 + n$ and performing regular linear regression, Ridge regression and Lasso regression.

Ridge Regression
$\begin{equation} \min_{w} \left\{||y-Xw||^2 +\lambda \sum_i w_i^2\right\} \end{equation}$

Lasso Regression
$\begin{equation} \min_{w} \left\{||y-Xw||^2 +\lambda \sum_i |w_i|\right\} \end{equation}$

In our simulation, for Ridge and Lasso regression, we are intentionally setting some extreme values of $\lambda$ so that we can see the feature selection characteristics of these regression. See this blog post for a very nice explanation of the behavior of Ridge and Lasso regression.

Note that, sklearn Ridge and Lasso doesn’t have lambda parameter, instead it has alpha parameter. My guess is, for Ridge lambda and alpha are the same. However, for Lasso, the description here is a bit confusing. After some trial and error, my suspicion is:

       alpha = number_of_samples x lambda

This is important for this analysis, since in the next section, we need to choose proper prior for our MCMC simulation depending on this value.

size = 1000 # number of data poins
np.random.seed(seed=1)

X_seed = np.random.normal(0, 1, size)
X1 = X_seed + np.random.normal(0, .1, size)
X2 = X_seed + np.random.normal(0, .1, size)
X3 = X_seed + np.random.normal(0, .1, size)

sigma = 1
noise = np.random.normal(0, sigma, size)

Y = 1 * X1 +  1 * X2 + 1 * X3 + noise

X = np.array([X1, X2, X3]).T

# Linear Regression
lr = LinearRegression()
lr.fit(X,Y)
print 'Linear model : {}'.format(lr.coef_)


# Ridge Regression (lamba = 1000)
ridge = Ridge(alpha=1000)
ridge.fit(X,Y)
print 'Ridge model : {}'.format(ridge.coef_)


# Lasso Regression
# From the description here http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html
# I am a little confused
# my guess is lambda = alpha * n_samples
lasso = Lasso(alpha=1.)
lasso.fit(X, Y)
print 'Lasso model : {}'.format(lasso.coef_)

Linear model : [ 1.16266223  0.98860861  0.8087923 ]
Ridge model : [ 0.73644275  0.72897954  0.73591734]
Lasso model : [ 0.89910385  0.          1.02094343]

MCMC Bayesian Regression

Uniform Prior

First, we assumed uniform prior for the regression co-efficients and perform the simulation:

# using uniform prior to find the co-efficient
w_min = -10
w_max = 10

with pm.Model() as uni:
    w1 = pm.Uniform('w1', lower=w_min, upper=w_max)
    w2 = pm.Uniform('w2', lower=w_min, upper=w_max)
    w3 = pm.Uniform('w3', lower=w_min, upper=w_max)

    wTx = w1*X1 + w2*X2 + w3*X3

    y = pm.Normal('y', mu=wTx, sd=sigma, observed=Y)

    stepper=pm.Metropolis()
    traceuni = pm.sample(100000, step=stepper)

 69%|██████▉   | 69407/100500 [00:48<00:21, 1434.44it/s]

Once finished, we can plot and get summary statistics as follows:

pm.traceplot(traceuni[20000::50])

enter image description here

pm.summary(traceuni[20000::50])

w1:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  1.207            0.268            0.023            [0.609, 1.688]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.644          1.033          1.208          1.397          1.733


w2:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.938            0.273            0.025            [0.399, 1.407]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.400          0.764          0.952          1.147          1.408


w3:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.819            0.262            0.022            [0.304, 1.371]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.275          0.650          0.812          0.991          1.355

We can also try to calculate the MAP estimate of the co-efficients. This should be the same as ML estimate in the last section.

with uni:
    uni_map = pm.find_MAP()
print(uni_map)

logp = -1,447.3, ||grad|| = 4.4401: 100%|██████████| 16/16 [00:00<00:00, 1157.33it/s]  

{'w3_interval__': array(0.16224552703292178), 'w1_interval__': array(0.23723549815233705), 'w3': array(0.8094527703753798), 'w2': array(0.9728674588105903), 'w1': array(1.1806453839461994), 'w2_interval__': array(0.19519086212979697)}

Bayesian Prior - Ridge Regression

Here, we are making sure that the prior distribution of the co-efficients have zero mean and $\sigma^2 / \lambda$ variance so that it gives us the same MAP estimate as in sklearn Ridge regression earlier.

alpha = 1000. # we used this value for sklearn Ridge estimation
lambda_1 = alpha
sigma = 1
sd = np.sqrt((sigma**2)/lambda_1)
print(sd)

with pm.Model() as ridge:
    w1 = pm.Normal('w1', mu=0, sd=sd)
    w2 = pm.Normal('w2', mu=0, sd=sd)
    w3 = pm.Normal('w3', mu=0, sd=sd)

    wTx = w1*X1 + w2*X2 + w3*X3

    ys = pm.Normal('ys', mu=wTx, sd=sigma, observed=Y)

    stepper=pm.Metropolis()
    traceridge = pm.sample(100000, step=stepper)

0.0316227766017

100%|██████████| 100500/100500 [01:11<00:00, 1402.93it/s]

pm.traceplot(traceridge[20000::50])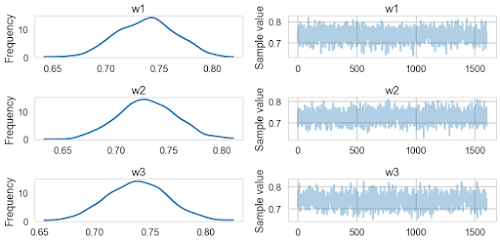

enter image description here

pm.summary(traceridge[20000::50])

w1:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.738            0.028            0.001            [0.683, 0.789]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.684          0.718          0.739          0.757          0.791


w2:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.729            0.027            0.001            [0.675, 0.779]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.676          0.711          0.729          0.748          0.783


w3:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.738            0.027            0.001            [0.687, 0.794]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.684          0.719          0.738          0.756          0.792

We can also estimate the MAP values for the co-efficients.

with ridge:
    mapridge = pm.find_MAP()
mapridge

{'w1': array(0.7377441385493746),
 'w2': array(0.7297896623054996),
 'w3': array(0.7369597481542057)}

Note that, these values are similar to the values obtained from sklearn Ridge.

Laplacian Prior - Lasso Regression

Note that, I am guessing the value of $\lambda$ here due to the mismatch between the Lasso equation and sklearn implementation. The conversion in the first few line ensure that we select proper $b$ for our Laplacian priors.

alpha=1. # we used this value for sklearn Lasso
lambda_1 = alpha  * size # my guess here is, lambda = alpha x num_samples

sigma = 1.

b = sigma**2 / lambda_1
print(b)

with pm.Model() as lasso:
    w1 = pm.Laplace('w1', mu=0, b=b)
    w2 = pm.Laplace('w2', mu=0, b=b)
    w3 = pm.Laplace('w3', mu=0, b=b)

    wTx = w1*X1 + w2*X2 + w3*X3

    ys = pm.Normal('ys', mu=wTx, sd=sigma, observed=Y)

    stepper=pm.Metropolis()
    tracelaplace = pm.sample(100000, step=stepper)

0.001
100%|██████████| 100500/100500 [01:14<00:00, 1343.27it/s]

pm.traceplot(tracelaplace[20000::50])

enter image description here

pm.summary(tracelaplace[20000::50])

w1:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.859            0.241            0.019            [0.412, 1.322]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.389          0.695          0.863          1.034          1.304


w2:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.179            0.141            0.009            [-0.001, 0.453]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.007          0.068          0.145          0.255          0.551


w3:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.890            0.237            0.020            [0.461, 1.371]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.421          0.725          0.891          1.053          1.345

We can also find the MAP estimate:

with lasso:
    maplasso = pm.find_MAP()
maplasso

{'w1': array(0.9500293027663775),
 'w2': array(1.3861762347993195e-09),
 'w3': array(0.9796505403007957)}

Note that, this values are similar to the values estimated using sklearn Lasso earlier.

Shafi's ML Blog

Sunday, December 3, 2017

Bayesian Regression using PyMC3

Linear regression

Prior Distribution

Linear Regression using sklearn

MCMC Bayesian Regression

Uniform Prior

Bayesian Prior - Ridge Regression

Laplacian Prior - Lasso Regression

No comments:

Post a Comment