PLSA using EM

Probabilistic Latent Semantic Analysis (PLSA)

• Paper note

  

We have:

• Documents Set $C=\{d_1,d_2,\ldots\}$
• Vocabulary Set $V=\{w_1,w_2\ldots\}$
• $k$ Topics $\{z_1,z_2,\ldots,z_k\}$

We want to find:

• Topic Word Distribution: Word distribution the topics, $\{p(w|z_i)\}$ for all $w\in V$ and $i=1,\ldots,k$ with the constraint $\sum_{w\in V}p(w|z_i)=1$.
• Document Topic Coverage: Coverage of each topics for document $d$, $\{p(z_i|d)\}$ all for $d\in C$ and $i=1,\ldots,k$ with constraint $\sum_{j=1}^k p(z_j|d) =1$.

For the rest of the note, I am skipping the background distribution for ease of mathematical notations. We define, parameter set $\Lambda =\{p(z_j|d), p(w|z_j)\}$, for $w\in V, d\in C, j=1,\ldots,k$. Marginal likelihood of this problem can be written as follows:

$$\begin{eqnarray} &&\arg\max_\Lambda \log p(C,W)\\ =&&\arg\max_\Lambda \sum_{d\in C}\sum_{w\in V}c(w,d)\log p(w,d)\\ =&&\arg\max_\Lambda \sum_{d\in C}\sum_{w\in V}c(w,d)\log p(w|d)p(d)\\ =&&\arg\max_\Lambda \sum_{d\in C}\sum_{w\in V}c(w,d)\log\sum_{j=1}^k p(w|z_j,d)p(z_j|d)\\ =&&\arg\max_\Lambda \sum_{d\in C}\sum_{w\in V}c(w,d)\log\sum_{j=1}^k p(w|z_j)p(z_j|d)\\ \end{eqnarray}$$
Here, $p(w|z_j,d)=p(w|z_j)$ since the word generation process doesn’t depend on the document, rather the topic.

E-step

$$\text{Set } q(z_j) = p(z_j|w,d)$$

Using Bayes Rule,
$$p(z_j|w,d)=\dfrac{p(w|z_j,d)p(z_j|d)}{\sum_{j=1}^k p(w|z_j,d)p(z_j|d)}=\dfrac{p(w|z_j)p(z_j|d)}{\sum_{j=1}^k p(w|z_j)p(z_j|d)}$$

M-step

$$\begin{eqnarray} &&\max _{\boldsymbol {\Lambda}}\sum_{d\in C}\sum_{w\in V}c(w,d) \sum_{j=1}^k {q(z_j)}\log p(w,d,z_j|\Lambda)\\ &&\max _{\boldsymbol {\Lambda}}\sum_{d\in C}\sum_{w\in V}c(w,d) \sum_{j=1}^k {q(z_j)}\log p(w|d,z_j)p(z_j|d)p(d)\\ &&\max _{\boldsymbol {\Lambda}}\sum_{d\in C}\sum_{w\in V}c(w,d) \sum_{j=1}^k {q(z_j)}\log p(w|z_j)p(z_j|d) \end{eqnarray}$$
Using Lagrange multipler,
$$\mathcal{H}=\sum_{d\in C}\sum_{w\in V}c(w,d) \sum_{j=1}^k {q(z_j)}\log p(w|z_j)p(z_j|d)+ \sum_{j=1}^k \tau_k (1-\sum_{w\in V}p(w|z_i))+ \sum_{d\in C}\rho_d(1-\sum_{j=1}^k p(z_j|d) )$$
We get:
$$p(w|z_j)=\dfrac{\sum_{d\in C} c(d,w)p(z_j|w,d)}{\sum_{w\in V}\sum_{d\in C} c(d,w)p(z_j|w,d)}$$
$$p(z_j|d)=\dfrac{\sum_{w\in V}c(d,w)p(z_j|w,d)}{\sum_{w\in V}c(d,w)}$$

Summary

• Initialize $\{p^{(0)}(z_j|d), p^{(0)}(w|z_j)\}$, for $w\in V, d\in C, j=1,\ldots,k$.

For Steps m=1, 2, … ,Do the following:

• E-step: For $i=1,\ldots,k$ and $d\in C$
  $$q^{(m)}(z_j)= p^{(m)}(z_j|w,d)=\dfrac{p^{(m)}(w|z_j)p^{(m)}(z_j|d)}{\sum_{j=1}^k p^{(m)}(w|z_j)p^{(m)}(z_j|d)}$$

• M-step:
  $$p^{(m+1)}(w|z_j)=\dfrac{\sum_{d\in C} c(d,w)p^{(m)}(z_j|w,d)}{\sum_{w\in V}\sum_{d\in C} c(d,w)p^{(m)}(z_j|w,d)}$$
  $$p^{(m+1)}(z_j|d)=\dfrac{\sum_{w\in V}c(d,w)p^{(m)}(z_j|w,d)}{\sum_{w\in V}c(d,w)}$$

GMM using EM

• • Gaussian Mixture Model (GMM)
  • E-step
  • M-step
  • Summary

Gaussian Mixture Model (GMM)

Similar to K-means clustering, however with a probabilistic flavor. That is, each point can belongs to more than one cluster, which is described by a probability distribution.

In the figure above, we will cluster the points using a mixture of 3 Gaussian distribution of the form $\mathcal{N}(\mu_k, \Sigma_k)$, $k=1,2,3$. The proportions of the Gaussian are given by $\{\pi_1, \pi_2, \pi_3\}$. Likelihood is defined as follows:
$$\begin{eqnarray} \prod_{i=1}^N p(X|\theta)=\pi_1 \mathcal{N}(x_i|\mu_1, \Sigma_1)+\pi_2 \mathcal{N}(x_i|\mu_2, \Sigma_2)+\pi_3 \mathcal{N}(x_i|\mu_3, \Sigma_3) \end{eqnarray}$$
We want to maximize the likelihood $\prod_{i=1}^N p(X|\theta)$, where $\theta =\{\mu_k, \Sigma_k, \pi_k\}$, $k=1,2,3$. We have the following constraint:
$$\Sigma_k\succeq0,~~~\pi_k\ge 0,~~~ \sum_k\pi_k=1$$

Due to the above constraints, it is difficult to solve the problem using methods like gradient descent. So, instead, we will use EM algorithm to solve this problem.
We will convert the above likelihood function to a marginal likelihood function by introducing latent variable $z_i\in\{1,2,3\}$ for $i=1,\ldots,N$. The marginal likelihood of GMM in this example as follows:
$$\begin{eqnarray} &&\text{marginal log likelihood}\\ &=&\sum_{i=1}^N\log p(x_i|\theta)\\ &=&\sum_{i=1}^N\log \sum_{z_i}p(x_i,z_i|\theta)\\ &=&\sum_{i=1}^N\log \sum_{k=1}^3 p(x_i|z_i=k,\theta)p(z_i=k|\theta)\\ \end{eqnarray}$$

Note that, here, we have a total of $3\times N$ probability values $p(z_i=k|\theta)$ associated with the latent variable $z_i$. However, GMM is a special case in that these mixture weights are same for all data points. So, we will only have 3 values. This is in contrast to method like PLSA, where the mixture weights are different for each data points. See here for GMM vs. PLSA. In addition, in GMM, $p(x_i|z_i=k,\theta)$ is represented by Gaussian.

GMM: Mixture weigths are same among all data points. Also $p(x_i|z_i=k,\theta)$ is Gaussian.
$$p(z_i=k|\theta)=\pi_k, ~~\text{for}~~i=1,\ldots,N$$
$$p(x_i|z_i=k,\theta)\sim\mathcal{N}(\mu_k, \Sigma_k)$$

E-step

For each $i$,
$$\text{Set } q(z_i) = p(z_i|x_i,\theta)$$

Using Bayes Rule,
$$p(z_i=k|x_i,\theta)=\dfrac{p(x_i|z_i=k,\theta)p(z_i=k|\theta)}{\sum_{k=1}^3 p(x_i|z_i=k,\theta)p(z_i=k|\theta)}=\dfrac{p(x_i|z_i=k,\theta)\pi_k}{\sum_{k=1}^3 p(x_i|z_i=k,\theta)\pi_k}$$

M-step

$$\begin{eqnarray} &&\max _{\boldsymbol {\theta}} \sum_{i=1}^N \sum_{z_i} {q(z_i)}\log p(x_i,z_i|\theta)\\ &=&\max _{\boldsymbol {\theta}} \sum_{i=1}^N \sum_{k=1}^3 {q(z_i=k)}\log p(x_i,z_i=k|\theta)\\ &=&\max _{\boldsymbol {\theta}} \sum_{i=1}^N \sum_{k=1}^3 {q(z_i=k)}\log [p(x_i|z_i=k,\theta) p(z_i=k|\theta)] \end{eqnarray}$$
Using the assumptions specific for GMM, we can re-write the above expression as follows for 1-D input data points:
$$\begin{eqnarray} &&\max _{\boldsymbol {\theta}} \sum_{i=1}^N \sum_{k=1}^3 {q(z_i=k)}\log \left[\dfrac{\exp(-(x_i-\mu_k)^2/2\sigma_k^2)}{Z} \pi_k\right]\\ &=&\max _{\boldsymbol {\theta}} \sum_{i=1}^N \sum_{k=1}^3 {q(z_i=k)} \left[\log\dfrac{\pi_k}{Z} -\dfrac{(x_i-\mu_k)^2}{2\sigma_k^2}\right] \end{eqnarray}$$
Now to determine $\theta =\{\mu_k, \Sigma_k, \pi_k\}$, we set derivative to zero.
$$\begin{eqnarray} \dfrac{\partial...}{\partial \mu_k}=\sum_{i=1}^N {q(z_i=k)}\dfrac{(x_i-\mu_k)}{\sigma_k^2}=0\\ \mu_k=\dfrac{\sum_{i=1}^N q(z_i=k) x_i}{\sum_{i=1}^N q(z_i=k)} \end{eqnarray}$$
Similarly,
$$\begin{eqnarray} \sigma_k=\dfrac{\sum_{i=1}^N q(z_i=k) (x_i-\mu_k)^2}{\sum_{i=1}^N q(z_i=k)} \end{eqnarray}$$
Solving $\pi_k$ is similar, however it also includes the constraint, $\sum_{k=1}^3 \pi_k=1$ and $\pi_k\ge0$.
$$\pi_k=\dfrac{\sum_{i=1}^N q(z_i=k) }{N}$$

Summary

• Initialize $\theta^{(0)} =\{\mu_k^{(0)}, \sigma_k^{(0)}, \pi_k^{(0)}\}$

For Steps m=1, 2, … ,Do the following:

• E-step: For $i=1,\ldots,N$
  $$q^{(m)}(z_i=k)=\dfrac{ \mathcal{N}(x_i|\mu_k^{(m)}, \sigma_k^{(m)})\pi_k^{(m)}}{\sum_{k=1}^3 \mathcal{N}(x_i|\mu_k^{(m)}, \sigma_k^{(m)})\pi_k^{(m)}}$$

• M-step:
  $$\mu_k^{(m+1)}=\dfrac{\sum_{i=1}^N q^{(m)}(z_i=k) x_i}{\sum_{i=1}^N q^{(m)}(z_i=k)}$$
  $$\sigma_k^{(m+1)}=\dfrac{\sum_{i=1}^N q^{(m)}(z_i=k) (x_i-\mu_k^{(m)})^2}{\sum_{i=1}^N q^{(m)}(z_i=k)}$$
  $$\pi_k^{(m+1)}=\dfrac{\sum_{i=1}^N q^{(m)}(z_i=k) }{N}$$

Expectation Maximization (EM) Algorithm

• Reference
• Objective of EM Algorithm
• General Idea
• E-step and KL divergence
• M Step
• Convergence

Reference

• CS 229 note
• Coursera course

Objective of EM Algorithm

From wikipedia,

In statistics, an expectation–maximization (EM) algorithm is an iterative method to find ML or MAP estimates of parameters in statistical models, where the model depends on unobserved latent variables.

In the statistical model, we have:

• $\mathbf {X}$ - observed data
• $\mathbf {Z}$ - unobserved latent data or missing value
• $\boldsymbol {\theta}$ - unknown parameters

Then:
$$\begin{equation} \text{likelihood} = L(\mathbf {X}, \mathbf {Z}, \boldsymbol {\theta}) = p(\mathbf {X}, \mathbf {Z}| \boldsymbol {\theta}) \end{equation}$$

Since, we do not observe $\mathbf {Z}$, we need to marginalize them out.

$$\begin{equation} \text{marginal likelihood} = L(\mathbf {X}, \boldsymbol {\theta}) = \int p(\mathbf {X}, \mathbf {Z}| \boldsymbol {\theta}) dZ = p(\mathbf {X}| \boldsymbol {\theta}) \end{equation}$$

In its general form, EM algorithm maximizes the marginal likelihood of the problem:

EM Objective $$\max_{ \boldsymbol {\theta}}p(\mathbf {X}| \boldsymbol {\theta})$$

General Idea

Suppose, we want to maximize the following marginal likelihood function:

Similar to variational inference, here, we approximate $p(\mathbf {X}| \boldsymbol {\theta})$ with a family of lower bounds $\mathcal{L}(\boldsymbol {\theta}, \boldsymbol {q})$. Here, $\boldsymbol {q}$ are known as variational parameters. In other words, we find the variational lower bounds as follows:
$$p(\mathbf {X}| \boldsymbol {\theta})\ge \mathcal{L}(\boldsymbol {\theta}, \boldsymbol {q}),~ \text{for any }\boldsymbol {q}$$

Initialization: Suppose, we start with point $\theta^k$ in the above figure.

E-step: We want to find the best lower bound from the family of lower bounds that goes through the point $\theta^k$.
$$q^{k+1} = \arg \max _q \mathcal{L}(\theta^k, q)$$
The red lower bound in the figure below is the best lower bound that goes through the point $\theta^k$.

M-step: Once we found the best lower bound at E-step, as shown above, we want to find the point $\theta^{k+1}$ that maximizes the lower bound.
$$\theta^{k+1}= \arg \max _{\theta} \mathcal{L}(\theta, q^{k+1})$$
As shown in the figure below, $\theta^{k+1}$ is the new point.

Continue Iteration: As shown in the figure below.

E-step and KL divergence

$$\begin{eqnarray} \text{marginal log likelihood}&=&\log p(\mathbf {X}| \boldsymbol {\theta})\\ &=&\sum_{i=1}^N\log p(x_i|\theta)\\ && [\text{assuming }N \text{ independent input points}]\\ &=&\sum_{i=1}^N\log \sum_{z_i} p(x_i,z_i|\theta)\\ &=&\sum_{i=1}^N\log \sum_{z_i} \dfrac{q_i(z_i)}{q_i(z_i)}p(x_i,z_i|\theta)\\ &=&\sum_{i=1}^N\log \sum_{z_i} q(z_j) \dfrac{p(x_i,z_j|\theta)}{q(z_j)}\\ &=&\sum_{i=1}^N\log \mathbb{E} _{q_i(z_i)}\left[\dfrac{p(x_i,z_i|\theta)}{q_i(z_i)}\right]\\ &\ge&\sum_{i=1}^N \mathbb{E} _{q_i(z_i)}\left[\log \dfrac{p(x_i,z_i|\theta)}{q(z_i)} \right]\\ &&\left[\text{Jensen's Inequality}~ f(\mathbb{E}[X])\ge \mathbb{E}[f(X)] ~\text{for concave}~ f\right]\\ \sum_{i=1}^N\log p(x_i|\theta)&\ge&\sum_{i=1}^N \sum_{z_i} {q_i(z_i)}\log \dfrac{p(x_i,z_i|\theta)}{q_i(z_i)} \end{eqnarray}$$

Now, in E-step, we are trying to approximate the marginal likelihood $p(\mathbf {X}| \boldsymbol {\theta})$ with a family of distribution $\mathcal{L}(\boldsymbol {\theta}, \boldsymbol {q})$. We want to choose a distribution, that minimizes the gap shown in the figure:

Now, if we set Jensen’s lower bound from the above to the approximation function, i.e. $\mathcal{L}(\boldsymbol {\theta}, \boldsymbol {q})=\sum_{i=1}^N \sum_{z_i} {q_i(z_i)}\log \dfrac{p(x_i,z_i|\theta)}{q_i(z_i)}$, then the gap becomes:

$$\begin{eqnarray} \text{gap} &=& \sum_{i=1}^N\log p(x_i|\theta)-\sum_{i=1}^N \sum_{z_i} {q_i(z_i)}\log \dfrac{p(x_i,z_i|\theta)}{q_i(z_i)} \\ &=&\sum_{i=1}^N\log p(x_i|\theta)\sum_{z_i} {q_i(z_i)}-\sum_{i=1}^N \sum_{z_i} {q_i(z_i)}\log \dfrac{p(x_i,z_i|\theta)}{q_i(z_i)} \\ &&[\text{Since} \sum_{z_i} {q_i(z_i)}=1]\\ &=&\sum_{i=1}^N \sum_{z_i} {q_i(z_i)}\left[\log p(x_i|\theta)-\log \dfrac{p(x_i,z_i|\theta)}{q_i(z_i)} \right]\\ &=&\sum_{i=1}^N \sum_{z_i} {q_i(z_i)}\log \dfrac{p(x_i|\theta)q_i(z_i)}{p(x_i,z_i|\theta)}\\ &=&\sum_{i=1}^N \sum_{z_i} {q_i(z_i)}\log \dfrac{p(x_i|\theta)q_i(z_i)}{p(x_i|\theta)p(x_i|z_i,\theta)}\\ &=&\sum_{i=1}^N \sum_{z_i} {q_i(z_i)}\log \dfrac{q_i(z_i)}{p(z_i|x_i,\theta)}\\ &=&\sum_{i=1}^N \text{KL}\left(q_i(z_i)||p(z_i|x_i,\theta)\right)\\ &\ge&0 \end{eqnarray}$$

Therefore, to minimize the gap, we will need $\sum_{i=1}^N \text{KL}$ to be zero, which will only happens when both the distributions are the same. Therefore, we have the following:
$$\begin{equation} \arg \max _{q_i(z_i)} \mathcal{L}(\theta, q)=p(z_i|x_i,\theta) \end{equation}$$

E-step
For each $i$,
$$\text{Set } q_i(z_i) = p(z_i|x_i,\theta)$$

M Step

In M-step, we want to find $\arg \max _{\boldsymbol {\theta}} \mathcal{L}(\boldsymbol {\theta}, \boldsymbol {q})$. Now,
$$\begin{eqnarray} \max _{\boldsymbol {\theta}} \mathcal{L}(\boldsymbol {\theta}, \boldsymbol {q})&=&\max _{\boldsymbol {\theta}} \sum_{i=1}^N \sum_{z_i} {q_i(z_i)}\log \dfrac{p(x_i,z_i|\theta)}{q_i(z_i)} \\ &=&\max _{\boldsymbol {\theta}} \left[\sum_{i=1}^N \sum_{z_i} {q_i(z_i)}\log p(x_i,z_i|\theta) -\sum_{i=1}^N \sum_{z_i} {q_i(z_i)}\log {q_i(z_i)}\right ]\\ &=&\max _{\boldsymbol {\theta}} \sum_{i=1}^N \sum_{z_i} {q_i(z_i)}\log p(x_i,z_i|\theta)\\ &=&\max _{\boldsymbol {\theta}} \sum_{i=1}^N \mathbb{E}_{q_i(\mathbf {z_i})}\log p(x_i, z_i|{\theta}) \end{eqnarray}$$

Summary

In summary:
We approximate the marginal log-likelihood using a family of lower bound:

$$\text{marginal log-likelihood}=\log p(\mathbf {X}| \boldsymbol {\theta})\ge \mathcal{L}(\theta, q)=\mathbb{E}_{q(\mathbf {Z})}\log\dfrac{P(\mathbf {X},\mathbf {Z}| \boldsymbol {\theta})}{q(\mathbf {Z})}$$

In E-step, we find best approximation of the lower bound, by maximizing over this family of lower bound, so that the gap between the marginal log-likelihood and the family of lower bound is minimized:

$$q^*(\mathbf {Z}) = \arg\max_{q(\mathbf {Z})}\mathcal{L}(\theta, q)=\arg\max_{q(\mathbf {Z})}\mathbb{E}_{q(\mathbf {Z})}\log\dfrac{P(\mathbf {X},\mathbf {Z}| \boldsymbol {\theta})}{q(\mathbf {Z})}=P(\mathbf {Z}|\mathbf {X}, \boldsymbol {\theta})$$

It turns out, the gap between marginal log-likelihood and the lower bound is equal to the KL divergence between the lower bound and $p(\mathbf {Z}|\mathbf {X}, \boldsymbol {\theta})$
.

$$\text{Gap} = \log p(\mathbf {X}| \boldsymbol {\theta})- \mathcal{L}(\theta, q)=\text{KL}(q(\mathbf {Z})||p(\mathbf {Z}|\mathbf {X}, \boldsymbol {\theta}))$$

In M-step, we maximize the best approximation of the lower bound to find the best $\boldsymbol {\theta}$.

$$\boldsymbol {\theta}^* = \arg\max_{\boldsymbol {\theta}}\mathcal{L}(\boldsymbol {\theta}, q^*)=\arg\max_{\boldsymbol {\theta}}\mathbb{E}_{q^*(\mathbf {Z})}\log\dfrac{P(\mathbf {X},\mathbf {Z}| \boldsymbol {\theta})}{q^*(\mathbf {Z})}=\arg\max_{\boldsymbol {\theta}}\mathbb{E}_{q^*(\mathbf {Z})}\log{P(\mathbf {X},\mathbf {Z}| \boldsymbol {\theta})}$$

Convergence

EM algortihm converges to a local maxima.

In the figure above, at point $\theta^k$, we chose the best lower bound curve $\mathcal{L}(\theta, q^{k+1})$ during E-step. At M-step, we found $\theta^{k+1}$ where the lower bound $\mathcal{L}(\theta, q^{k+1})$ is maximum. The likelihood at point $\theta^{k+1}$ is $\log p(X|\theta^{k+1})$ which is definitely higher than or equal to the lower bound at that point, i.e. $\mathcal{L}(\theta^{k+1}, q^{k+1})$.
$$\begin{eqnarray} \log p(X|\theta^{k+1})&\ge&\mathcal{L}(\theta^{k+1}, q^{k+1})\ge\mathcal{L}(\theta^{k}, q^{k+1})=\log p(X|\theta^{k})\\ &&\log p(X|\theta^{k+1})\ge\log p(X|\theta^{k})\ \end{eqnarray}$$

That is the likelihood value at step k+1 is higher than the value at step k. That is, at each step, EM algorithm doesn’t lower the likelihood function. This can also be used as debugging tool.

Bayesian Regression using PyMC3

• Linear regression
  • Prior Distribution
• Linear Regression using sklearn
• MCMC Bayesian Regression
  • Uniform Prior
  • Bayesian Prior - Ridge Regression
  • Laplacian Prior - Lasso Regression

Linear regression

$$\begin{eqnarray} y_i= \boldsymbol{x}_i^T \boldsymbol{w} +n_i \\ \end{eqnarray}$$
Here, $n_i \sim \mathcal{N}(0, \sigma^2)$. Therefore, we can re-write $y_i$ as:
$$\begin{eqnarray} y_i\sim\mathcal{N}(\boldsymbol{x}_i^T \boldsymbol{w}, \sigma^2) \end{eqnarray}$$

In Bayesian linear regression, we assume $y_i, \boldsymbol{x}_i$ as data and $\boldsymbol{w}, \sigma^2$ as parameters. Therefore, the likelihood is as follows:
$$\begin{eqnarray} \text{likelihood} = p(y| \boldsymbol{x},\boldsymbol{w},\sigma)=\prod_{i=1}^n p(y_i| \boldsymbol{x}_i,\boldsymbol{w},\sigma) \end{eqnarray}$$

Using Bayes rule, the posterior distribution can be written as:
$$\begin{eqnarray} p(\boldsymbol{w},\sigma|y, \boldsymbol{x})=\dfrac{ p( y|\boldsymbol{w},\sigma, \boldsymbol{x})p(\boldsymbol{w},\sigma|\boldsymbol{x})}{p(y|\boldsymbol{x})} \propto p( y|\boldsymbol{w},\sigma, \boldsymbol{x})p(\boldsymbol{w},\sigma|\boldsymbol{x})\\ p(\boldsymbol{w},\sigma|y)\propto p( y|\boldsymbol{w},\sigma)p(\boldsymbol{w},\sigma)~~~[\text{re-writing without }\boldsymbol{x}] \end{eqnarray}$$

Now, we can assume $\boldsymbol{w}$ and $\sigma$ to be independent of each other. We can further assume, all the elements of $\boldsymbol{w}=\left[w_1, \ldots, w_m\right]$ are independent. Therefore, prior can be written as:

$$\begin{eqnarray} p(\boldsymbol{w},\sigma) = \prod_j p(w_j) ~p(\sigma) \end{eqnarray}$$

Prior Distribution

• When ${w_j}\sim\mathcal{N}\left(0,\dfrac{\sigma^2}{\lambda }\right)$, then the MAP estimate is ridge regression.

• When $p(w_j)=\dfrac{1}{2(\sigma^2 / \lambda)}\exp\left(-\dfrac{|w_j|}{ \sigma^2 / \lambda}\right)$, i.e. Laplacian distribution, then the MAP estimate is the lasso regression.

---

Linear Regression using sklearn

First we import all the necessary functions:

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("whitegrid")
sns.set_context("poster")

from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso, LassoCV
from sklearn.linear_model import Ridge, RidgeCV
import pymc3 as pm

We are generating some data points for the function $y= x_1 + x_2 + x_3 + n$ and performing regular linear regression, Ridge regression and Lasso regression.

Ridge Regression
$$\begin{equation} \min_{w} \left\{||y-Xw||^2 +\lambda \sum_i w_i^2\right\} \end{equation}$$

Lasso Regression
$$\begin{equation} \min_{w} \left\{||y-Xw||^2 +\lambda \sum_i |w_i|\right\} \end{equation}$$

In our simulation, for Ridge and Lasso regression, we are intentionally setting some extreme values of $\lambda$ so that we can see the feature selection characteristics of these regression. See this blog post for a very nice explanation of the behavior of Ridge and Lasso regression.

Note that, sklearn Ridge and Lasso doesn’t have lambda parameter, instead it has alpha parameter. My guess is, for Ridge lambda and alpha are the same. However, for Lasso, the description here is a bit confusing. After some trial and error, my suspicion is:

       alpha = number_of_samples x lambda

This is important for this analysis, since in the next section, we need to choose proper prior for our MCMC simulation depending on this value.

size = 1000 # number of data poins
np.random.seed(seed=1)

X_seed = np.random.normal(0, 1, size)
X1 = X_seed + np.random.normal(0, .1, size)
X2 = X_seed + np.random.normal(0, .1, size)
X3 = X_seed + np.random.normal(0, .1, size)

sigma = 1
noise = np.random.normal(0, sigma, size)

Y = 1 * X1 +  1 * X2 + 1 * X3 + noise

X = np.array([X1, X2, X3]).T

# Linear Regression
lr = LinearRegression()
lr.fit(X,Y)
print 'Linear model : {}'.format(lr.coef_)


# Ridge Regression (lamba = 1000)
ridge = Ridge(alpha=1000)
ridge.fit(X,Y)
print 'Ridge model : {}'.format(ridge.coef_)


# Lasso Regression
# From the description here http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html
# I am a little confused
# my guess is lambda = alpha * n_samples
lasso = Lasso(alpha=1.)
lasso.fit(X, Y)
print 'Lasso model : {}'.format(lasso.coef_)

Linear model : [ 1.16266223  0.98860861  0.8087923 ]
Ridge model : [ 0.73644275  0.72897954  0.73591734]
Lasso model : [ 0.89910385  0.          1.02094343]

---

MCMC Bayesian Regression

Uniform Prior

First, we assumed uniform prior for the regression co-efficients and perform the simulation:

# using uniform prior to find the co-efficient
w_min = -10
w_max = 10

with pm.Model() as uni:
    w1 = pm.Uniform('w1', lower=w_min, upper=w_max)
    w2 = pm.Uniform('w2', lower=w_min, upper=w_max)
    w3 = pm.Uniform('w3', lower=w_min, upper=w_max)

    wTx = w1*X1 + w2*X2 + w3*X3

    y = pm.Normal('y', mu=wTx, sd=sigma, observed=Y)

    stepper=pm.Metropolis()
    traceuni = pm.sample(100000, step=stepper)

 69%|██████▉   | 69407/100500 [00:48<00:21, 1434.44it/s]

Once finished, we can plot and get summary statistics as follows:

pm.traceplot(traceuni[20000::50])

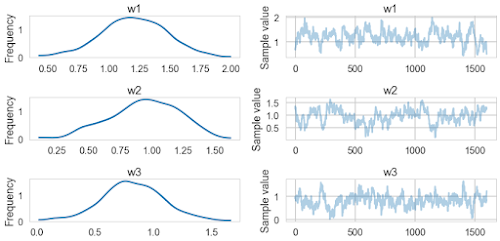
pm.summary(traceuni[20000::50])

w1:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  1.207            0.268            0.023            [0.609, 1.688]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.644          1.033          1.208          1.397          1.733


w2:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.938            0.273            0.025            [0.399, 1.407]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.400          0.764          0.952          1.147          1.408


w3:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.819            0.262            0.022            [0.304, 1.371]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.275          0.650          0.812          0.991          1.355

We can also try to calculate the MAP estimate of the co-efficients. This should be the same as ML estimate in the last section.

with uni:
    uni_map = pm.find_MAP()
print(uni_map)

logp = -1,447.3, ||grad|| = 4.4401: 100%|██████████| 16/16 [00:00<00:00, 1157.33it/s]  

{'w3_interval__': array(0.16224552703292178), 'w1_interval__': array(0.23723549815233705), 'w3': array(0.8094527703753798), 'w2': array(0.9728674588105903), 'w1': array(1.1806453839461994), 'w2_interval__': array(0.19519086212979697)}

Bayesian Prior - Ridge Regression

Here, we are making sure that the prior distribution of the co-efficients have zero mean and $\sigma^2 / \lambda$ variance so that it gives us the same MAP estimate as in sklearn Ridge regression earlier.

alpha = 1000. # we used this value for sklearn Ridge estimation
lambda_1 = alpha
sigma = 1
sd = np.sqrt((sigma**2)/lambda_1)
print(sd)

with pm.Model() as ridge:
    w1 = pm.Normal('w1', mu=0, sd=sd)
    w2 = pm.Normal('w2', mu=0, sd=sd)
    w3 = pm.Normal('w3', mu=0, sd=sd)

    wTx = w1*X1 + w2*X2 + w3*X3

    ys = pm.Normal('ys', mu=wTx, sd=sigma, observed=Y)

    stepper=pm.Metropolis()
    traceridge = pm.sample(100000, step=stepper)

0.0316227766017

100%|██████████| 100500/100500 [01:11<00:00, 1402.93it/s]

pm.traceplot(traceridge[20000::50])

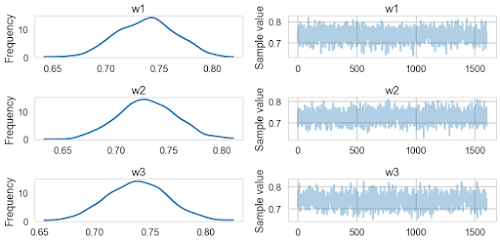
pm.summary(traceridge[20000::50])

w1:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.738            0.028            0.001            [0.683, 0.789]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.684          0.718          0.739          0.757          0.791


w2:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.729            0.027            0.001            [0.675, 0.779]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.676          0.711          0.729          0.748          0.783


w3:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.738            0.027            0.001            [0.687, 0.794]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.684          0.719          0.738          0.756          0.792

We can also estimate the MAP values for the co-efficients.

with ridge:
    mapridge = pm.find_MAP()
mapridge

{'w1': array(0.7377441385493746),
 'w2': array(0.7297896623054996),
 'w3': array(0.7369597481542057)}

Note that, these values are similar to the values obtained from sklearn Ridge.

Laplacian Prior - Lasso Regression

Note that, I am guessing the value of $\lambda$ here due to the mismatch between the Lasso equation and sklearn implementation. The conversion in the first few line ensure that we select proper $b$ for our Laplacian priors.

alpha=1. # we used this value for sklearn Lasso
lambda_1 = alpha  * size # my guess here is, lambda = alpha x num_samples

sigma = 1.

b = sigma**2 / lambda_1
print(b)

with pm.Model() as lasso:
    w1 = pm.Laplace('w1', mu=0, b=b)
    w2 = pm.Laplace('w2', mu=0, b=b)
    w3 = pm.Laplace('w3', mu=0, b=b)

    wTx = w1*X1 + w2*X2 + w3*X3

    ys = pm.Normal('ys', mu=wTx, sd=sigma, observed=Y)

    stepper=pm.Metropolis()
    tracelaplace = pm.sample(100000, step=stepper)

0.001
100%|██████████| 100500/100500 [01:14<00:00, 1343.27it/s]

pm.traceplot(tracelaplace[20000::50])

pm.summary(tracelaplace[20000::50])

w1:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.859            0.241            0.019            [0.412, 1.322]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.389          0.695          0.863          1.034          1.304


w2:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.179            0.141            0.009            [-0.001, 0.453]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.007          0.068          0.145          0.255          0.551


w3:

  Mean             SD               MC Error         95% HPD interval
  -------------------------------------------------------------------

  0.890            0.237            0.020            [0.461, 1.371]

  Posterior quantiles:
  2.5            25             50             75             97.5
  |--------------|==============|==============|--------------|

  0.421          0.725          0.891          1.053          1.345

We can also find the MAP estimate:

with lasso:
    maplasso = pm.find_MAP()
maplasso

{'w1': array(0.9500293027663775),
 'w2': array(1.3861762347993195e-09),
 'w3': array(0.9796505403007957)}

Note that, this values are similar to the values estimated using sklearn Lasso earlier.

Monte Carlo Sampling

• Reference
• Why use Monte Carlo Sampling?
• Inversion Method
• Rejection Sampling Method
• Importance Sampling
• Markov Chain Monte Carlo (MCMC)
  • Markov Chain
  • Metropolis-Hastings Algorithm
  • Gibbs Sampling

Reference

• Lecture video on sampling
• Coursera course
• UCBerkeley Note

---

Why use Monte Carlo Sampling?

1. To sample from a distribution $p(x)$ - often a posterior
2. To calculate $\mathbb{E}_{p(x)}\left[f(x)\right]=\int f(x)p(x)dx$

Here, 1 and 2 are related. If we can sample from $p(x)$, we can also calculate $\mathbb{E}_{p(x)}\left[f(x)\right]$ by application of law of large numbers. Suppose $\{{x^{(i)}}\}$ are i.i.d. samples drawn from $p(x)$. Then law of large number says:

$$\frac{1}{N}\sum_{i=1}^N f\left({x^{(i)}}\right) \xrightarrow{\text{a.s.}} \int f(x)p(x)dx$$

Properties of Monte Carlo Sampling

• Estimator is unbiased
• Variance shrinks $\propto \frac{1}{S}$

---

Inversion Method

• To sample from a distribution $p(y)$, use inverse of the CDF of the distribution and uniform random number generator.

• CDF of a distribution $p(y)$ is given as
  $$h(y) = \int_{-\infty}^y p(y')dy'$$

  

Steps:

• Draw a number from uniform generator $u \sim \text{Uniform}[0,1]$
• Assign this number as $h(y)$, i.e. $u=h(y)$. Then $$y = h^{-1}(y)$$

Cons:

• If we can’t compute $h^{-1}(y)$, then, we won’t be able to use this method.

---

Rejection Sampling Method

• To sample from $p(x)$, we consider another distribution $q(x)$ from which we can sample under the restriction $p(x) < Mq(x)$ - i.e., we are upper bounding the distribution $p(x)$ with $Mq(x)$.

Steps:

• Generate sample $x^{(i)}\sim q(x)$

• Accept this sample with a certain probability. How?

  • Generate sample from a uniform distribution $u \sim \left[0,Mq(x^{(i)})\right]$

  • Accept $x^{(i)}$ if $u\le p(x^{(i)})$
    Alternatively,

  • List item Generate sample from a uniform distribution $u \sim \left[0,1\right]$

  • Accept this sample if $u\le \frac{p(x^{(i)})$}{Mq(x^{(i)})}$

This method accepts $\frac{1}{M}$ points on average.

Pros:

• Works for most distributions (even unnormalized).
• Even works if we know our distribution up to normalization constant as it happens in probabilistic modeling, i.e. if we know $\frac{p(x)}{Z}$, then we can upper bound by $p(x)\le Z Mq(x)$ and use this method to perform sampling.

Cons:

• In higher dimension, $M$ is high. Then, this method rejects most of the points.

---

Importance Sampling

Unlike Inversion method or Rejection sampling, here goal is to compute $\mathbb{E}_{p(x)}\left[f(x)\right]=\int f(x)p(x)dx$ directly.

Steps:

• Sample from a different distribution $x^{(i)}\sim q(x)$
• Define importance weight $w(x^{(i)})=\frac{p(x^{(i)})}{q(x^{(i)})}$
• Then, $\mathbb{E}_{p(x)}\left[f(x)\right]$ is in fact $\frac{1}{N}\sum_{i=1}^N f(x^{(i)})w(x^{(i)})$

Proof:

$$\begin{eqnarray} &&\frac{1}{N}\sum_{i=1}^N f(x^{(i)})w(x^{(i)}) \\ = &&\frac{1}{N}\sum_{i=1}^N f(x^{(i)})\frac{p(x^{(i)})}{q(x^{(i)})} \\ \xrightarrow {\text{a.s.}}&& \int \left(f(x)\frac{p(x)}{q(x)} \right) q(x) dx ~~\text{[law of large number]}\\ =&&\int f(x)p(x)dx \end{eqnarray}$$

• In practice, we would like to choose $q(x)$ as close as possible to $|f(x)|w(x)$ to reduce the variance of our estimator

---

Markov Chain Monte Carlo (MCMC)

Rejection sampling and importance samplings performs poorly in higher dimensions. So, instead we use MCMC sampling.

Markov Chain

See this book for details.

• In first order Markov chain, transition to next state depends only on previous state. A stochastic process $X_0, X_1,\ldots$ satisfies the Markov Property if
  $$P\{X_{n+1}=i_{n+1}|X_n=i_n,X_{n-1}=i_{n-1},\ldots,X_0=i_0\}=P\{X_{n+1}=i_{n+1}|X_n=i_n\}$$
• For Markov chain, we have initial state $S$ and transition matrix $P$.

Here,
$$P=\begin{array}{r|lll} & L & R\\ \hline L & 0.3 & 0.7\\ R & 0.5 & 0.5 \end{array}$$

• Assuming the frog starts at $L$, i.e. $S=[1, ~ 0]$, then after $k$ steps, then the probability that the frog will be in $L$ or $R$ is given by
  $$S^{(k)}=SP^k$$
  We can also replace $S=[1, ~ 0]$ with a probability vector to represent the initial state - i.e. $S=[0.5, ~ 0.5]$, the frog is equally likely to start in either $L$ or $R$

Regular Markov Chain & Stationary Distribution

• A Markov chain is regular if all the entries in the transition matrix is non-zero (this is a sufficient condition, not necessary condition).
• For a regular Markov chain, long-range predictions are independent of the starting state, i.e. it doesn’t depend whether the frog started in $L$ or $R$. In other words, $SP^k=\pi$ for any choice of $S$ when $k\to\infty$. Here, $\pi$ is a stationary distribution such than $\pi = P\pi$. One interesting property is, all the entries in a column of $P^k$ will have the same value. E.g.
  $$\text{For}~~P= \left[ {\begin{array}{cc} 0.3 & 0.7 \\ 0.5 & 0.5 \\ \end{array} } \right], ~~~~~~ P^k\to \left[ {\begin{array}{cc} 0.417 & 0.583 \\ 0.417 & 0.583 \\ \end{array} } \right]$$
  And, $SP^k=\pi=[0.417, 0.583]$ for any probability vector $S$.

A distribution is said to be invariant/ stationary w.r.t. a Markov chain if
the transition function of that chain leaves that distribution unchanged. E.g. for a Markov chain with transition operator $T(x\to y)$, a distribution $\pi(x)$ is considered a stationary distribution if
$$\pi(y) = \sum_x \pi(x) T(x \to y)$$

Detailed Balance

A transition operator $T$ satisfies detailed balance if
$$\pi (x) T(x\to x') = \pi(x') T(x' \to x)$$
Here, $\pi(x)$ is the stationary distribution of state $x$, and $T(x\to y)$ the transition probability of moving from state $x$ to $y$.

How to design a Markov Chain with stationary distribution $\pi$

If a transition operator satisfies detailed balance w.r.t. a particular
distribution, then that distribution will be invariant under T. In other words,
$$\text{If}~~~~ \pi(x) T(x\to y) = \pi(y) T(y\to x), \\ \text{Then}~~~~ \pi(y) =\sum_x \pi(x) T(x\to y)$$
Proof:
$$\sum_x \pi(x) T(x\to y)=\sum_x \pi(y) T(y\to x)=\pi(y) \sum_x T(y\to x)=\pi(y)$$

Therefore, to design a Markov Chain w.r.t. a stationary distribution $\pi$, find a transition operator $T$ such that it satisfies the detailed balance w.r.t. $\pi$.

How to use Markov Chain for Sampling?

• We want to sample from $p(x)$
• Build a Markov chain that converge to $p(x)$
  
  • Start from any $x^0$
  • For $k = 0, 1,\ldots$
    $x^{k+1}\sim T(x^k \to x^{k+1})$
  • Eventually $x^k$ will look like samples from $p(x)$
    Here $T(x^k \to x^{k+1})$ is the transition probability from state $k$ to $k+1$.

---

Metropolis-Hastings Algorithm

This is somewhat similar to the idea of rejection sampling to Markov chain. We start with a wrong Markov Chain, and introduce a Critic. Critic ensures that the random walk does not go too far away from the desired distribution.

For k=1,2,$\ldots$
– Sample $x'$ from wrong $Q(x^k\to x')$
– Accept proposal $x'$ with probability $A(x^k\to x')$
– Otherwise stay at $x^k$
$$x^{k+1}=x^k$$

Transition probability of the above algorithm is as follows:
$$T(x\to y) = Q(x\to y) A(x\to y)~~\text{when}~~x\ne y\\ T(x\to x) = Q(x\to x) A(x\to x) + \sum_{y\ne x} Q(x \to y) (1-A(x\to y))$$

How to choose critic $A$

We choose critic $A$ such that the transition probability $T$ as described above converged to the desired distribution $\pi$. We can use detailed balance for this purpose:
$$\begin{eqnarray} \pi(x) T(x\to y) &=& \pi(y) T(y\to x)\\ \pi(x) Q(x\to y) A(x\to y) &=& \pi(y) Q(y\to x)A(y\to x)\\ \dfrac{A(x\to y) }{A(y\to x)}&=&\dfrac{ \pi(y) Q(y\to x)}{\pi(x)Q(x\to y)}=\rho \end{eqnarray}$$
Now, we assign, $A(y\to x)=1$, then $A(x\to y) =\rho$ as long as $\rho\le 1$. When $\rho > 1$, we can simply choose 1. I.e.

$$A(x\to y) =\min\left\{ 1,\dfrac{ \pi(y) Q(y\to x)}{\pi(x)Q(x\to y)} \right\}$$

Things to note:

• We are only using ratio of the desired distribution $\frac{\pi(y)}{\pi(x)}$ - this means, we don’t need to know the exact distribution. So, no issue with the normalization constant.
• Choice of $Q$:
  
  • $Q(x\to y) > 0$
  • $Q$ should spread out, i.e. $Q$ with high variance will give us un-correlated samples. But this also means, the probability of rejection will increase. On the other had, $Q$ with low variance will take long time to converge. See the following figures:

---

Gibbs Sampling

We want to sample from a joint distribution $p(x,y,z)$

Initialize $x=x_0$, $y=y_0$, $z=z_0$.
For $k=0, 1, 2, \ldots$
$$\begin{eqnarray} x_{k+1} &\sim& p(x|y=y_k, z=z_k)\\ y_{k+1} &\sim& p(y|x=x_{k+1}, z=z_k)\\ z_{k+1} &\sim& p(z|x=x_{k+1}, z=z_{k+1})\\ \end{eqnarray}$$

The 1D marginal distributions in the above algorithm can be calculated analytically or using something like rejection sampling.

Why Gibbs Sampling works?

We need to prove that the above mentioned sampling steps actually converge to stationary distribution $p(x,y,z)$. In other words, we need to prove:
$$p(x',y',z') = \sum_{x,y,z} p(x,y,z) T(x,y,z \to x'y'z')$$

Proof:
$$\begin{eqnarray} &&\sum_{x,y,z} p(x,y,z) T(x,y,z \to x'y'z')\\ =&&\sum_{x,y,z} p(x,y,z) p(x'|y=y, z=z) p(y'|x=x',z=z) p(z'|x=x',y=y')\\ =&&p(z'|x',y')\sum_{x,y,z} p(x,y,z) p(x'|y, z) p(y'|x',z) \\ =&&p(z'|x',y')\sum_{y,z} \left[ p(x'|y, z) p(y'|x',z) \sum_x p(x,y,z)\right]\\ =&&p(z'|x',y')\sum_{y,z} \left[ p(x'|y, z) p(y,z) p(y'|x',z) \right]\\ =&&p(z'|x',y')\sum_{y,z} \left[ p(x',y, z) p(y'|x',z) \right]\\ =&&p(z'|x',y')\sum_{z} \left[ p(y'|x',z) \sum_y p(x',y, z)\right]\\ =&&p(z'|x',y')\sum_{z} \left[ p(y'|x',z) p(x', z)\right]\\ =&&p(z'|x',y')\sum_{z} p(y',x',z) \\ =&&p(z'|x',y') p(y',x') \\ =&&p(x',y',z') \\ \end{eqnarray}$$

Metropolis-Hastings vs. Gibbs

Gibbs sampling generate highly correlated samples and takes long time to converge. Also, since sampling of each dimension depends on the past sampling from other dimension, the scheme is not parallel. Its possible to make it parallel as follows:
$$\begin{eqnarray} x_{k+1} &\sim& p(x|y=y_k, z=z_k)\\ y_{k+1} &\sim& p(y|x=x_{k}, z=z_k)\\ z_{k+1} &\sim& p(z|x=x_{k}, z=z_{k})\\ \end{eqnarray}$$
However, this does not guarantee that the samples will converge to the desired distribution $p(x,y,z)$. So, alternative is to sample from the above and use it as a proposal in Metropolis-hastings where the critic will decide whether or not to accept this point. Since, the above is pretty close the the desired distribution $p(x,y,z)$, there is a higher chance that the critic will accept this point.

Notes on Bayesian Inference

• Reference
• Bayes Theorem
  • Bayesian Netwok (Graphical Model)
• Calculation of Posterior Distribution
• Conjugate Prior
• Variational Inference
  • Steps:
  • Minimizing the KL divergence
• Mean Field Approximation
• Common Probability Distributions
  • Gamma Distribution
  • Beta Distribution

Reference

• Coursera course
• UC Berkeley Note
• Stanford Note

Bayes Theorem

We have,

• $~\theta~$: Parameters
• $~X~$: Observations

Bayes rules is as follows:

Probability rules:

• Sum rules: Marginalization from joint distribution $$p(X) = \int_{-\infty}^\infty p(X,Y) dY$$
• Chain rules:
  $$\begin{eqnarray} P(X, Y) &=& P(X|Y)P(Y)=P(Y|X)P(X) \\ P(X,Y,Z)&=&P(X|Y,Z)P(Y,Z)=P(X|Y,Z)P(Y|Z)P(Z)\\ P(X_1,\ldots,X_N)&=&\prod_{i=1}^NP(X_i|X_1,\ldots,X_{i-1}) \end{eqnarray}$$

Point Estimation (Frequentist vs. Bayesian)

Rather than estimate the entire distribution $p(θ|x)$, sometimes it is sufficient to find a single ‘good’ value for $θ$. We call this a point estimate.

• Frequentist thinks parameters $\theta$ are fixed, data $X$ are random.
  Maximum Likelihood Estimation: $$\hat{\theta}=\arg\max_{\theta} P(X|\theta)$$
• Bayesian thinks parameters $\theta$ are random, data $X$ are fixed.
  Maximum Aposteriori Estimation (MAP) $$\hat{\theta}=\arg\max_{\theta} P(\theta|X)$$
  
  • MAP estimation is not invariant to non-linear transformations of $θ$. E.g. A non-linear transformation $\theta^\prime=g(\theta)$, to $\theta$ can shift the posterior mode in such a way that $g^{-1}(\mathrm{mode}[\theta^\prime]) \neq \mathrm{mode}[\theta]$.
  • MAP estimate may not be typical of the posterior.

Bayesian Netwok (Graphical Model)

• Nodes are random variables
• Edges indicates dependence (e.g. Grass is wet depends on both sprinkler or rain, and whether sprinkler is on or off depends on rain)
• Observed variables are shaded nodes; unshaded nodes are hidden
• Plated denote replicated structure

Joint probability over all the variables in the above model is given by:

Example 1:

Here, $P(S,R,G) = P(G|S, R) P(S|R) P(R)$

Example 2: Naive Bayes Classifer

Joint Probability $P(c, f_1,\ldots,f_N)=P(c)\prod_{i=1}^N P(f_i|C)$

In plate notation, the figure above can be shortened as follows:

Calculation of Posterior Distribution

• Analytical approach: Use of conjugate prior
• Converting to optimization problem: variational inference (mean field approximation)
• Simulations: MCMC methods (metropolis-hastings or gibbs sampling) - see next post.

Since variational inference approximate the posterior, MCMC usually produce higher accuracy - however may be slower to converge, as shown in the figure below:

Conjugate Prior

• MIT lecture note has a good section on conjugate prior

Point estimation is useful for many applications, however true goal in Bayesian analysis is often to find the full posterior $p(\theta|X)$. In most cases, it is difficult to calculate the denominator $p(X)=\int p(X|\theta)p(\theta)$. One approach to circumventing the integral is to use conjugate priors. Here the idea is, if we choose the ‘right’ prior for a particular likelihood function, then we can compute the posterior without worrying about the integral.

Formally, a prior $p(\theta)$ is conjugate to the likelihood $p(X|\theta)$, if the prior $p(\theta)$ and the posterior $p(\theta|x)$ are from the same family of distribution.

Examples:

• Beta distribution is conjugate to Bernoulli likelihood. Here is a good example of this for baseball batting average calculation.
• Dirichlet distribution is conjugate to Multinomial likelihood (e.g. application in LDA)

Variational Inference

• Very intuitive explanation in this blog
• Very nice notes on the derivation from CMU here.

If there are no conjugate prior, it might be hard to calculate the posterior. In many cases, we can approximate the posterior with some known distributions.

Steps

We want to find posterior $p(\theta|X)$

• Select a family of distribution $Q=\{q(\theta|\phi)\}$ parameterized by $\phi$.
• Find the best approximation of $p(\theta|X)$ from $Q$ by minimizing the KL divergence between the two.

$$\begin{equation} p(\theta|X)\approx q^*(\theta|\phi) ={\arg\min}_{q(\theta|\phi)\in Q} KL[q(\theta|\phi)||p(\theta|X)] \end{equation}$$

Will there be issue with denominator integral?

Due to the use of KL divergence, we will have:
$$\min_{q(\theta|\phi)\in Q} KL[q(\theta|\phi)||p(\theta|X)]= \min_{q(\theta)\in Q} KL[q(\theta|\phi)||{\hat{p} (\theta|X)}]$$
where ${p} (\theta|X) = \dfrac{\hat{p} (\theta|X)}{Z}$. So, we don’t have to worry about $Z$.

Evidence Lower Bound (ELBO)

Evidence lower bound is defined as:

$$\text{ELBO}=\mathbb{E}_q[\log p(x, z)]-\mathbb{E}_q[\log q(z)]$$

Properties: . $\log p(x)\ge \text{ELBO}$

Proof:
$$\begin{eqnarray} \log p(x)&=& \log \int_z p(x, z) dx= \log \int_z q(z) \dfrac{p(x, z)}{q(z)}dz\\ &=&\log\mathbb{E}_q\left[\dfrac{p(x, z)}{q(z)}\right]\ge\mathbb{E}_q[\log p(x, z)]-\mathbb{E}_q[\log q(z)] \\ &&\left[\text{Jensen's Inequality}~ f(\mathbb{E}[X])\ge \mathbb{E}[f(X)]\right] \end{eqnarray}$$

Minimizing the KL divergence

We can write the KL divergence as:
$$\begin{eqnarray} &&KL(q(z)||p(z|x))\\ &=& \int_z q(z) \log \dfrac{q(z)}{p(z|x)}= \mathbb{E}_{q}\left[\log \dfrac{q(z)}{p(z|x)}\right]\\ &=&\mathbb{E}_{q} [\log q(z)]-\mathbb{E}_{q} [\log p(z|x)]\\ &=& \mathbb{E}_{q} [\log q(z)] - \mathbb{E}_{q} [\log p(z, x)]+\mathbb{E}_{q}[\log p(x)]\\ &=& \mathbb{E}_{q} [\log q(z)] - \mathbb{E}_{q} [\log p(z, x)] +\log p(x)\\ &=& -\text{ELBO}+\log p(x)\\ \end{eqnarray}$$

Therefore,
$$\min_{q}KL(q||p) =\min_{q}\left[-\text{ELBO}+\log p(x)\right]=\max_{q}\left[\text{ELBO}\right]$$

In words, any $q$ that maximizes ELBO, minimizes KL divergence.

$$\begin{equation} p(Z|X)\approx q^*(Z) ={\arg\min}_{q(Z)} KL[q(Z)||p(Z|X)]={\arg\max}_{q(Z)} \mathbb{E}_q[\log p(x, z)]-\mathbb{E}_q[\log q(z)] \end{equation}$$

Mean Field Approximation

In mean field approximation, the family of distribution $Q$ is assumed to factorize over the components of $\mathbf{z}$, i.e. $z_1, z_2, \ldots$
$$Q = \left\{ q(\mathbf{z}|\phi) = \prod_{i=1}^{d}q(z_i)\right\}$$
and we are trying to achieve

$$\begin{eqnarray} &&\min_{q} \ \mbox{KL}[ q(\mathbf{z}|\phi) \ || \ p(\mathbf{z}|X) ]\\ &=&\min_{q} \ \mbox{KL}\left[ \prod_{i}q(z_i) \ || \ p(\theta|X) \right]\\ &=&\max_{q}\left\{ \text{ELBO}= \mathbb{E}_{q} \log p(z, x) -\mathbb{E}_{q} \log q(z)\right\}\\ &=&\max_{q}\left[ \sum_{i} \mathbb{E}_{q_i} \log p(z_i|z_{-i}, x)-\sum_i \mathbb{E}_{q_i} \log q_i(z_i)\right] \end{eqnarray}$$
To get to the last line from the previous line, we did the following math:
$$\begin{eqnarray} \mathbb{E}_{q} [\log q(z)] &=&\mathbb{E}_{q} \left[\sum_i\log q_i(z_i)\right]=\sum_i \mathbb{E}_{q_i} \left[\log q_i(z_i)\right] \end{eqnarray}$$
And,
$$\begin{eqnarray} p(z, x)= p(z_1,\ldots, z_d,x)&=& p(z_1,\ldots, z_d|x)p(x)= p(x) \prod_{i=1}^d p(z_i|z_{1:i-1}, x)\\ \mathbb{E}_{q} [\log p(z,x)]&=&\log p(x) + \sum_{i=1}^d \mathbb{E}_{q} [\log p(z_i|z_{1:i-1}, x)] \end{eqnarray}$$

Co-ordinate Ascent

We can solve this using co-ordinate ascent algorithm, by maximizing a single factor $q_k$, while keeping all other factors $q_{-k}$ constant.
$$\begin{eqnarray} q_k^*&=&\arg\max_{q_k} \left[-\mathbb{E}_{q_k} \left[\log q_k(z_k)\right] + \mathbb{E}_{q} \left[\log p(z_k|z_{-k}, x)\right]\right]\\ &=&\arg\max_{q_k}\left[-\int_{z_k} q_k \log q_k dz_k +\int_z q(z) p(z_k|z_{-k}, x) dz\right]\\ &=&\arg\max_{q_k}\left[-\int_{z_k} q_k \log q_k dz_k +\int_{z_k} q_k \int_{z_{j\ne k}} \prod_{j\ne k}q_j p(z_k|z_{-k}, x) dz_{j\ne k} dz_k\right]\\ &=&\arg\max_{q_k}\left[-\int_{z_k} q_k \log q_k dz_k +\int_{z_k} q_k \mathbb{E}_{-k} [p(z_k|z_{-k}, x)] dz_k\right]\\ \dfrac{d \mathcal{L}}{d q_k^*}&=&-\log q_k^* + \mathbb{E}_{-k} [p(z_k|z_{-k}, x)] -1 =0\\ q_k^*&\propto&\exp\left\{\mathbb{E}_{-k} [p(z_k|z_{-k}, x)] \right\}=\exp\left\{\mathbb{E}_{-k} \left[\dfrac{p(z_k|z_{-k}, x)p(z_k)}{p(z_k)}\right] \right\}\\ q_k^*&\propto&\exp\left\{\mathbb{E}_{-k} [p(z_k,z_{-k}, x)] \right\} \end{eqnarray}$$

$$\begin{eqnarray} q(z_k)&\propto&\mathbb{E}_{q_{-k}}\log p(z_k|z_{-k},x)\\ &\propto&\mathbb{E}_{q_{-k}}\log p(z_k,z_{-k},x) \end{eqnarray}$$

In summary, we first defined a family of approximations called mean field approximations, in which there are no dependencies between latent variables . Then we decomposed the ELBO into a nice form under mean field assumptions. Then, we derived a coordinate ascent updates to iteratively optimize each local variational approximation under mean field assumptions.

Common Probability Distributions

Gamma Distribution

$$p(\gamma|a,b) = \dfrac{b^a}{\Gamma(a)}\gamma ^{a-1}e^{-b\gamma}$$
Here,

• $\gamma, a, b > 0$
• support of Gamma distribution is $[0, \infty)$
• $\mathbb{E}[\gamma]=\frac{a}{b}$
• $\text{Var}[\gamma]=\frac{a}{b^2}$

Example: Suppose I ran 5km $\pm$ 100 m every day, i.e. mean 5km with std 100m. We can model this as Gamma distribution. We can also use Gaussian - however, that means we can run negative distance.

Beta Distribution

$$p(x|a,b)=\dfrac{1}{B(a,b)}x^{a-1}(1-x)^{b-1}$$
Here,
- a, b > 0
- support of beta distribution is [0,1], i.e. $x\in [0,1]$
- $\mathbb{E}[x]=\frac{a}{a+b}$
- $\text{Var}[x]=\frac{ab}{(a+b)^2(a+b-1)}$

Example: Baseball batting average (its a number between 0 and 1). e.g.$0.27\pm 0.1$